Matemática

Descripción

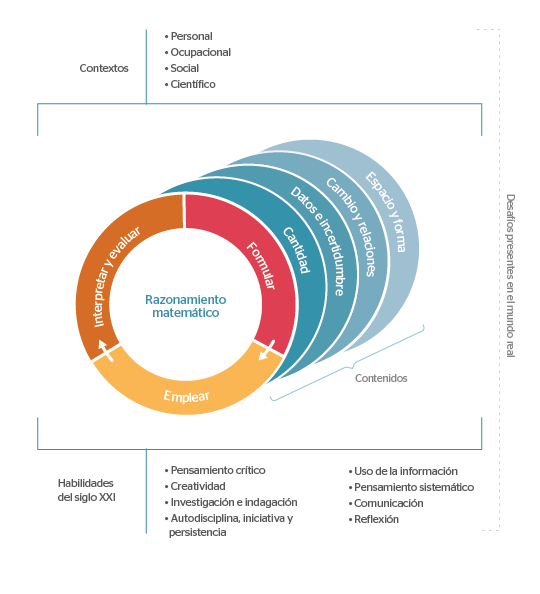
El marco de Matemática de PISA 2022 define los fundamentos teóricos de la evaluación de matemática de PISA, basado en el concepto fundamental de competencia matemática, relacionando el razonamiento matemático y los tres procesos del ciclo de resolución de problemas (modelamiento matemático). El marco describe cómo se organiza el conocimiento del contenido matemático en cuatro categorías de contenido. También describe cuatro categorías de contextos en los que los estudiantes enfrentarán desafíos matemáticos.

La evaluación PISA mide la eficacia con la que los países están preparando a los estudiantes para utilizar las matemáticas en todos los aspectos de su vida personal, cívica y profesional, como parte de su ciudadanía constructiva, comprometida y reflexiva del siglo XXI.

¿Qué es la competencia matemática?

La competencia matemática es la capacidad de un individuo para razonar matemáticamente y para formular, emplear e interpretar las matemáticas para resolver problemas en una variedad de contextos del mundo real. Incluye utilizar conceptos, procedimientos, datos y herramientas para describir, explicar y predecir fenómenos. De esta forma, ayuda a las personas a conocer el rol que tienen las matemáticas en el mundo y a emitir juicios y decisiones adecuadamente fundadas que los ciudadanos constructivos, comprometidos y reflexivos del siglo XXI necesitan.

Lo nuevo en PISA 2022

PISA 2022 tiene como objetivo considerar las matemáticas en un mundo que cambia rápidamente impulsado por nuevas tecnologías y tendencias, en que los ciudadanos son creativos y están comprometidos, haciendo juicios no rutinarios sobre sí mismos y la sociedad en que viven. Esto resalta la capacidad de razonar matemáticamente, que siempre ha sido parte del marco de PISA. Este cambio de tecnología está creando también la necesidad en los estudiantes de comprender aquellos conceptos de pensamiento computacional que son parte de la competencia matemática. Por último, el marco reconoce que la mayoría de los estudiantes pueden acceder a evaluaciones por computadora mejoradas en PISA.

Razonamiento matemático

La capacidad de razonar lógicamente y presentar argumentos de manera honesta y convincente es una habilidad que se está volviendo cada vez más importante en el mundo actual. Las matemáticas son una ciencia sobre objetos y nociones bien definidos que pueden ser analizados y transformados de diferentes formas utilizando el “razonamiento matemático” para obtener conclusiones ciertas y atemporales.

Con las matemáticas, los estudiantes aprenden que, con razonamientos y suposiciones adecuados, pueden llegar a resultados en los que pueden confiar plenamente como verdaderos en una amplia variedad de contextos de la vida real. También es importante que estas conclusiones sean imparciales, sin necesidad de validación por parte de una autoridad externa.

Concepciones clave

Al menos seis concepciones clave proporcionan estructura y apoyo al razonamiento matemático. Estas incluyen:

comprender la cantidad, los sistemas numéricos y sus propiedades algebraicas
apreciar el poder de la abstracción y la representación simbólica
ver estructuras matemáticas y sus regularidades
reconocer relaciones funcionales entre cantidades
utilizar modelos matemáticos como lentes del mundo real (por ejemplo, los que surgen en las ciencias físicas, biológicas, sociales, económicas y del comportamiento); y
entender la variación como el corazón de la estadística.

Utilice las flechas para revisar los contenidos clave en profundidad:

CANTIDAD, SISTEMAS NUMÉRICOS Y SUS PROPIEDADES ALGEBRAICAS

La noción fundamental y antigua de cantidad se expresa en las matemáticas a través del concepto de sistemas numéricos y de las propiedades algebraicas básicas que emplean estos sistemas. La abrumadora universalidad de esos sistemas los hace esenciales para la competencia matemática.

También es importante entender cuestiones de representación (como símbolos que involucran números, como puntos en una recta numérica o como cantidades geométricas) y cómo moverse entre ellos; las formas en que estas representaciones se ven afectadas por los sistemas numéricos; y las formas en que las propiedades algebraicas de estos sistemas son relevantes para operar dentro de los sistemas.
LAS MATEMÁTICAS COMO SISTEMA BASADO EN LA ABSTRACCIÓN Y LA REPRESENTACIÓN SIMBÓLICA

Las ideas fundamentales de las matemáticas han surgido de la experiencia humana en el mundo y de la necesidad de dotar de coherencia, orden y previsibilidad a esa experiencia. Muchos objetos matemáticos modelan la realidad, o al menos reflejan aspectos de la realidad de alguna manera. La abstracción implica prestar atención deliberada y selectivamente a las similitudes estructurales entre los objetos y construir relaciones entre esos objetos en función de estas similitudes. En las matemáticas escolares, la abstracción forma relaciones entre objetos concretos, representaciones simbólicas y operaciones, incluidos algoritmos y modelos mentales.

Los estudiantes usan representaciones, ya sean simbólicas, gráficas, numéricas o geométricas, para organizar y comunicar su pensamiento matemático. Las representaciones pueden condensar significados y procesos matemáticos en algoritmos eficientes. Las representaciones también son un elemento central del modelamiento matemático, lo que permite a los estudiantes abstraer una formulación simplificada o idealizada de un problema de la vida real.
ESTRUCTURAS MATEMÁTICAS Y SUS REGULARIDADES

La estructura está íntimamente relacionada con la representación simbólica. El uso de símbolos es poderoso, pero solo si adquieren significado para el que los usa, en lugar de convertirse en objetos sin sentido para ser reorganizados en una página. Ver la estructura es una forma de encontrar y recordar el significado de una representación abstracta. Ser capaz de ver la estructura es una ayuda conceptual importante para el conocimiento puramente procedimental.

Un sentido sólido de la estructura matemática también respalda el modelamiento. Cuando los objetos bajo estudio no son objetos matemáticos abstractos, sino objetos del mundo real para ser modelados por las matemáticas, entonces la estructura matemática puede guiar el modelamiento. Los estudiantes también pueden aplicar estructuras a objetos no matemáticos para someterlos a análisis matemático.
RELACIONES FUNCIONALES ENTRE CANTIDADES

Las relaciones entre cantidades se pueden expresar con ecuaciones, gráficos, tablas o descripciones verbales. Un paso importante en el aprendizaje es extraer de estos la noción de una función en sí misma, como un objeto abstracto del cual estos son representaciones.

Las dos vistas de una función, la vista ingenua como un proceso y la vista más abstracta como objeto se pueden reconciliar en el gráfico de la función. Pero leer un gráfico, coordinar los valores en los ejes, también tiene un aspecto dinámico o de proceso. Y la gráfica de una función es una herramienta importante para explorar la noción de tasa de cambio. El gráfico proporciona una herramienta visual para comprender una función como una relación entre cantidades covariantes.
EL MODELAMIENTO MATEMÁTICO COMO LENTE DEL MUNDO REAL

Los modelos representan una conceptualización ideal de un fenómeno científico o de la vida real. Son, en ese sentido, abstracciones de la realidad. Un modelo puede presentar una conceptualización que se entiende como una aproximación o hipótesis de trabajo sobre el fenómeno objeto o puede ser una simplificación intencional. Los modelos matemáticos se formulan en lenguaje matemático y utilizan una amplia variedad de herramientas y resultados matemáticos (por ejemplo, de la aritmética, el álgebra o la geometría). Por lo tanto, se utilizan como formas de definir con precisión la conceptualización o teoría de un fenómeno, para analizar y evaluar datos (¿el modelo se ajusta a los datos?) y para hacer predicciones. Los modelos se pueden operar, es decir, hacer que se ejecuten a lo largo del tiempo o con entradas variables, produciendo así una simulación. Cuando se hace esto, puede ser posible hacer predicciones, estudiar consecuencias y evaluar la idoneidad y precisión de los modelos.
LA VARIACIÓN COMO EL CORAZÓN DE LA ESTADÍSTICA

Los seres vivos y los no vivos varían respecto de muchas de sus características. Esta variación es típicamente grande y, como resultado, es difícil hacer generalizaciones sin precisar de alguna manera hasta qué punto se mantiene esa generalización. La contabilidad de la variabilidad es uno de los elementos definitorios, si no el central, en torno al cual se basa la disciplina de la estadística. En el mundo de hoy, las personas a menudo se enfrentan a este tipo de situaciones simplemente ignorando la variación. Como resultado, sugieren amplias generalizaciones que a menudo son engañosas, si no incorrectas, y por lo tanto muy peligrosas. El sesgo en el sentido de las ciencias sociales generalmente se produce cuando no se tiene en cuenta la variabilidad de la característica particular en discusión.

La estadística es, en muchos sentidos, una búsqueda de patrones en un contexto muy variable: tratar de encontrar la señal que define la "verdad" en medio de una gran cantidad de ruido aleatorio. La “verdad” se pone entre comillas porque no es la verdad platónica que las matemáticas pueden ofrecer, sino una estimación de la verdad puesta en un contexto probabilístico, acompañada de una estimación del error contenido en el proceso. En última instancia, quien toma las decisiones se enfrenta al dilema de no saber nunca con certeza cuál es la verdad. La estimación al final es un conjunto de valores plausibles.

Formular

La palabra formular en la definición de competencia matemática se refiere a la capacidad de las personas para reconocer e identificar oportunidades para usar las matemáticas y luego proporcionar una estructura matemática a un problema presentado en alguna forma contextualizada. En el proceso de formular situaciones matemáticamente, los individuos determinan de dónde pueden extraer las matemáticas esenciales para analizar, plantear y resolver el problema. Ellos traducen de un entorno del mundo real al dominio de las matemáticas y se proporciona al problema del mundo real una estructura matemática, representaciones y especificidad. Ellos razonan y dan sentido a las restricciones y suposiciones en el problema. En concreto, este proceso de formulación matemática de situaciones incluye actividades como las siguientes:

seleccionar un modelo apropiado de una lista; **
identificar los aspectos matemáticos de un problema situado en un contexto de la vida real e identificar las variables significativas;
reconocer la estructura matemática (incluyendo regularidades, relaciones y patrones) en problemas o situaciones;
simplificar una situación o problema para que sea susceptible de análisis matemático;
identificar restricciones y suposiciones detrás de cualquier modelo matemático y simplificaciones extraídas del contexto;
representar una situación matemáticamente, usando variables, símbolos, diagramas y modelos estándar apropiados;
representar un problema de una manera diferente, incluye organizarlo de acuerdo con conceptos matemáticos y hacer suposiciones apropiadas;
comprender y explicar las relaciones entre el lenguaje específico del contexto de un problema y el lenguaje simbólico y formal necesario para representarlo matemáticamente;
traducir un problema al lenguaje matemático o a una representación;
reconocer aspectos de un problema que se corresponden con problemas conocidos o conceptos, hechos o procedimientos matemáticos;
usar tecnología (como una hoja de cálculo o la función de lista en una calculadora gráfica) para representar una relación matemática inherente a un problema contextualizado; y
crear una serie ordenada de instrucciones (paso a paso) para resolver problemas.

** Esta actividad se incluye en la lista para resaltar la necesidad de que los desarrolladores de ítems de la prueba incluyan ítems que sean accesibles para los estudiantes en el extremo inferior de la escala de rendimiento.

Emplear

La palabra emplear en la definición de competencia matemática se refiere a la capacidad de las personas para aplicar conceptos matemáticos, datos, procedimientos y razonamientos para resolver problemas formulados matemáticamente para obtener resultados matemáticos. En el proceso de emplear conceptos matemáticos, datos, procedimientos y razonamientos para resolver problemas, las personas realizan los procedimientos matemáticos necesarios para obtener resultados y encontrar una solución matemática. Trabajan en un modelo de la situación del problema, establecen regularidades, identifican conexiones entre entidades matemáticas y crean argumentos matemáticos. Específicamente, este proceso incluye actividades como:

realizar un cálculo simple; **
sacar una conclusión simple; **
seleccionar una estrategia apropiada de una lista; **
diseñar e implementar estrategias para encontrar soluciones matemáticas;
usar herramientas matemáticas, incluida la tecnología, para ayudar a encontrar soluciones exactas o aproximadas;
aplicar hechos matemáticos, reglas, algoritmos y estructuras al encontrar soluciones;
manipular números, gráficos y datos estadísticos, expresiones algebraicas y ecuaciones, y representaciones geométricas;
hacer diagramas, gráficos y construcciones matemáticas y extraer información matemática de ellos;
usar y cambiar entre diferentes representaciones en el proceso de encontrar soluciones;
hacer generalizaciones basadas en los resultados de aplicar procedimientos matemáticos para encontrar soluciones;
reflexionar sobre argumentos matemáticos y explicar y justificar resultados matemáticos; y
evaluar la importancia de los patrones y regularidades observados (o propuestos) en los datos.

** Esta actividad se incluye en la lista para resaltar la necesidad de que los desarrolladores de ítems de la prueba incluyan ítems que sean accesibles para los estudiantes en el extremo inferior de la escala de rendimiento.

Interpretar y evaluar

La palabra interpretar (y evaluar) utilizada en la definición de competencia matemática se centra en la capacidad de los individuos para reflexionar sobre soluciones, resultados o conclusiones matemáticas e interpretarlos en el contexto del problema de la vida real que inició el proceso. Esto implica traducir las soluciones matemáticas o el razonamiento involucrado al contexto del problema y determinar si los resultados son razonables y tienen sentido en el contexto del problema.

Específicamente, este proceso de interpretación, aplicación y evaluación de resultados matemáticos incluye actividades como las siguientes:

interpretar información presentada en forma gráfica y/o diagramas; **
evaluar un resultado matemático en términos del contexto; **
interpretar un resultado matemático en el contexto del mundo real;
evaluar la razonabilidad de una solución matemática en el contexto de un problema del mundo real;
comprender cómo el mundo real afecta los resultados y los cálculos de un procedimiento o modelo matemático para poder emitir juicios contextuales sobre cómo deben ajustarse o aplicarse los resultados;
explicar por qué un resultado o conclusión matemática tiene o no sentido dado el contexto de un problema;
comprender el alcance y los límites de los conceptos matemáticos y las soluciones matemáticas;
criticar e identificar los límites del modelo utilizado para resolver un problema; y
usar el pensamiento matemático y el pensamiento computacional para hacer predicciones, proporcionar evidencia para argumentos y probar y comparar soluciones propuestas.

** Esta actividad se incluye en la lista para resaltar la necesidad de que los desarrolladores de ítems de prueba incluyan ítems que sean accesibles para los estudiantes en el extremo inferior de la escala de rendimiento.

Conocimiento del contenido

Una comprensión del contenido matemático y la capacidad de aplicar ese conocimiento para resolver problemas contextualizados significativos son importantes para los ciudadanos en el mundo moderno. Es decir, para razonar matemáticamente y resolver problemas e interpretar situaciones en contextos personales, ocupacionales, sociales y científicos, las personas necesitan recurrir a ciertos conocimientos y comprensión matemáticos.

Las siguientes categorías de contenido utilizadas en PISA desde 2012 se utilizan nuevamente en PISA 2022 para reflejar los fenómenos matemáticos que subyacen a amplias clases de problemas, la estructura general de las matemáticas y las principales líneas de los currículos escolares típicos:

cambio y relaciones,
espacio y forma,
cantidad, y
datos e incertidumbre.

Se han identificado cuatro temas para un énfasis especial en la evaluación PISA 2022. Estos temas no son nuevos en las categorías de contenido de matemáticas. En cambio, estos son temas que merecen especial énfasis:

fenómenos de crecimiento (cambio y relaciones),
aproximación geométrica (espacio y forma),
simulaciones computarizadas (cantidad), y
toma de decisiones condicional (datos e incertidumbre).

Cantidad

La noción de cantidad puede ser el aspecto matemático más generalizado y esencial para relacionarnos y funcionar en nuestro mundo. Incorpora la cuantificación de atributos de objetos, relaciones, situaciones y entidades en el mundo; la comprensión de varias representaciones de esas cuantificaciones; y la evaluación de interpretaciones y argumentos basados en la cantidad. Comprometerse con la cuantificación del mundo implica comprender medidas, conteos, magnitudes, unidades, indicadores, tamaño relativo y tendencias y patrones numéricos.

La cuantificación es un método principal para describir y medir un amplio conjunto de atributos de aspectos del mundo. Permite el modelamiento de situaciones, el análisis de cambios y relaciones, la descripción y manipulación del espacio y la forma, la organización e interpretación de datos y la medición y evaluación de la incertidumbre.

Simulaciones por computadora

Tanto las matemáticas como las estadísticas involucran problemas que no se resuelven tan fácilmente porque las matemáticas requeridas son complejas o involucran una gran cantidad de factores que operan en el mismo sistema. Cada vez más en el mundo actual, estos problemas se abordan mediante simulaciones por computadora impulsadas por algoritmos matemáticos.

Identificar las simulaciones por computadora como un punto focal de la categoría de contenido de cantidad indica que, en el contexto de la evaluación de matemáticas basada en computadora, existe una amplia categoría de problemas complejos. Por ejemplo, los estudiantes pueden usar simulaciones por computadora para analizar el presupuesto y la planificación como parte de un ítem de la prueba.

Datos e incertidumbre

En la ciencia, la tecnología y la vida cotidiana, la incertidumbre es un hecho. Por lo tanto, la incertidumbre es un fenómeno en el corazón del análisis matemático de muchas situaciones problemáticas, y la teoría de la probabilidad y la estadística, así como las técnicas de representación y descripción de datos, se han establecido para tratarla. Este contenido de datos e incertidumbre incluye reconocer el lugar de la variación en los procesos, tener una idea de la cuantificación de esa variación, reconocer la incertidumbre y el error en la medición y saber sobre el azar. También incluye formar, interpretar y evaluar conclusiones extraídas en situaciones donde la incertidumbre es central. La cuantificación es un método principal para describir y medir un amplio conjunto de atributos de aspectos del mundo.

Toma de decisiones condicional

Identificar la toma de decisiones condicional como un punto focal del contenido de incertidumbre y datos indica que se debe esperar que los estudiantes aprecien cómo las suposiciones hechas al establecer un modelo afectan las conclusiones que se pueden obtener y que diferentes supuestos/relaciones podrían resultar en una conclusión diferente.

Cambio y relaciones

Lo natural y diseñado en el mundo muestran una multitud de relaciones temporales y permanentes entre objetos y circunstancias, donde ocurren cambios dentro de sistemas de objetos interrelacionados o en circunstancias donde los elementos se influencian unos a otros. En muchos casos, estos cambios ocurren con el tiempo. En otros casos, los cambios en un objeto o cantidad están relacionados con cambios en otro objeto. Algunas de estas situaciones implican un cambio discreto; otras implican un cambio continuo. Algunas relaciones son de naturaleza permanente o invariable. Saber más sobre el cambio y las relaciones implica comprender los tipos fundamentales de cambio y reconocer cuándo ocurren para utilizar modelos matemáticos adecuados para describir y predecir el cambio. Matemáticamente, esto significa modelar el cambio y las relaciones con funciones y ecuaciones apropiadas, así como crear, interpretar y traducir entre representaciones simbólicas y gráficas.

Fenómenos de crecimiento

Comprender los peligros de las pandemias de gripe y los brotes bacterianos, así como la amenaza del cambio climático, exige que las personas no solo piensen en términos de relaciones lineales, sino que reconozcan que tales fenómenos necesitan modelos no lineales que reflejen un crecimiento muy rápido. Las relaciones lineales son comunes y fáciles de reconocer y comprender, pero asumir la linealidad a veces puede ser peligroso.

Identificar los fenómenos de crecimiento como un punto focal del contenido de cambio y relaciones no indica una expectativa de que los estudiantes participantes hayan estudiado la función exponencial, y ciertamente los ítems no requerirán el conocimiento de la función exponencial. En cambio, la expectativa es que habrá ítems que esperan que los estudiantes reconozcan (a) que no todo el crecimiento es lineal y (b) que el crecimiento no lineal tiene implicaciones profundas sobre cómo entendemos ciertas situaciones.

Espacio y forma

El espacio y la forma abarcan una amplia gama de fenómenos que se encuentran en todas partes en nuestro mundo visual y físico: patrones, propiedades de los objetos, posiciones y orientaciones, representaciones de objetos, decodificación y codificación de información visual y navegación e interacción dinámica con formas reales, así como con representaciones. La geometría sirve como una base esencial para el espacio y la forma, pero la categoría se extiende más allá de la geometría tradicional en contenido, significado y método, basándose en elementos de otras áreas matemáticas como la visualización espacial, la medición y el álgebra.

Aproximación geométrica

El mundo de hoy está lleno de formas que no siguen los patrones típicos de uniformidad o simetría. Debido a que las fórmulas simples no se ocupan de la irregularidad, se ha vuelto más difícil comprender lo que vemos y encontrar el área o el volumen de las estructuras resultantes.

Identificar aproximaciones geométricas como un punto focal del contenido de espacio y forma señala la necesidad de que los estudiantes puedan usar su comprensión de los fenómenos tradicionales de espacio y forma en una variedad de situaciones típicas.

Contextos

Un aspecto importante de la competencia matemática es que las matemáticas se utilizan para resolver un problema planteado en un contexto. El contexto es el aspecto del mundo de un individuo en el que se sitúan los problemas. La elección de estrategias y representaciones matemáticas apropiadas a menudo depende del contexto en el que surge un problema. Para PISA, es importante que se utilice una amplia variedad de contextos.

Personal

Los problemas clasificados en la categoría de contexto personal se centran en las actividades propias, de la familia o del grupo de compañeros. Los contextos personales incluyen (pero no se limitan a) aquellos relacionados con la preparación de alimentos, compras, juegos, salud personal, transporte personal, deportes, viajes, programación personal y finanzas personales.

Ocupacional

Los problemas clasificados en la categoría de contexto ocupacional se centran en el mundo del trabajo. Los ítems categorizados como ocupacionales pueden incluir (pero no se limitan a) cosas tales como medir, calcular costos y pedir materiales para la construcción, nómina/contabilidad, control de calidad, programación/inventario, diseño/arquitectura y toma de decisiones relacionadas con el trabajo.

Los contextos ocupacionales pueden relacionarse con cualquier nivel de la fuerza laboral, desde trabajo no calificado hasta los niveles más altos de trabajo profesional, aunque los ítems de la evaluación PISA deben ser accesibles para estudiantes de 15 años.

Social

Los problemas clasificados en la categoría de contexto social se enfocan en la comunidad de uno (ya sea local, nacional o global). Pueden involucrar (pero no se limitan a) cosas tales como sistemas de votación, transporte público, gobierno, políticas públicas, demografía, publicidad, estadísticas nacionales y economía. Aunque los individuos están involucrados en todas estas cosas de manera personal, en la categoría de contexto social, el enfoque de los problemas está en la perspectiva de la comunidad.

Científico

Los problemas clasificados en la categoría científica se relacionan con la aplicación de las matemáticas al mundo natural y cuestiones y temas relacionados con la ciencia y la tecnología. Los contextos particulares pueden incluir (pero no se limitan a) áreas como el tiempo o el clima, la ecología, la medicina, la ciencia espacial, la genética, la medición y el propio mundo de las matemáticas. Los ítems que son intramatemáticos, donde todos los elementos involucrados pertenecen al mundo de las matemáticas, caen dentro del contexto científico.

Habilidades del siglo XXI

Existe un creciente interés a nivel mundial por lo que se denominan habilidades del siglo XXI y su posible inclusión en los sistemas educativos. La OCDE ha publicado un documento que se centra en tales habilidades y ha patrocinado un proyecto de investigación titulado “El futuro de la educación y las habilidades: Educación 2030”. Unos 25 países están involucrados en este estudio transnacional de currículos que incluye la incorporación de tales habilidades. El proyecto tiene como enfoque central cómo podría ser el plan curricular de estudios en el futuro, centrándose inicialmente en las matemáticas. Algunas de las habilidades clave del siglo XXI son:

pensamiento crítico;
creatividad;
investigación e indagación;
autodisciplina, iniciativa y persistencia;
uso de la información;
pensamiento sistemático;
comunicación; y
reflexión.

Aunque los desarrolladores de ítems de prueba reconocen estas habilidades del siglo XXI, los ítems de Matemática en PISA 2022 no se desarrollan específicamente de acuerdo con estas habilidades.